The Analytic Element Method (AEM)
An analytic element is a mathematical function that is associated with a particular boundary condition and it is a solution of the governing groundwater flow equations. One kind of element represents flow to a pumping well, a second kind represents discharge to a stream segment, a third kind represents an area of recharge, and so on. With the analytic element method (AEM), mathematical functions of numerous elements in a model are superposed (summed) to create a composite equation that may have as many as thousands of terms. This is similar in concept to the method of images covered in most groundwater textbooks, where a couple of well functions are superposed to simulate a well near a linear boundary,
Using computers to superpose large numbers of more sophisticated solutions in groundwater flow models (AEM) was an idea pioneered by Otto Strack. Readers interested in more thorough coverage of the theory of AEM will find it in textbooks by Strack (2017, 1989) and Haitjema (1995). A shorter summary of the AEM is covered in the general groundwater textbook (Fitts, 2023).
Unknown parameters are associated with most elements. For example, a head-specified well has one unknown parameter: the well discharge. Boundary condition equations are written for each unknown parameter, creating a system of simultaneous equations that is solved using standard solvers. In cases with non-linear equations, iteration is required to solve the system. The solved system results in composite equations for potential (head) and discharge that are functions of location and time; h(x,y,z,t) and q(x,y,z,t) . These composite equations are used to make head contour plots, trace pathlines, etc.
There are many computer programs that implement the analytic element method. They differ in many ways which can be baffling to those less familiar with the AEM. The following table comparing AEM modeling programs was assembled to help sift through the options.
Interview about Anaqsim and the AEM
Recently, Dr. Charlie Fitts, author of Anaqsim, was interviewed about the analytic element method, what inspired him to write Anaqsim, how Anaqsimdiffers from other AEM programs, and some other related topics. Here is a link to the interview.
AEM Software Compared
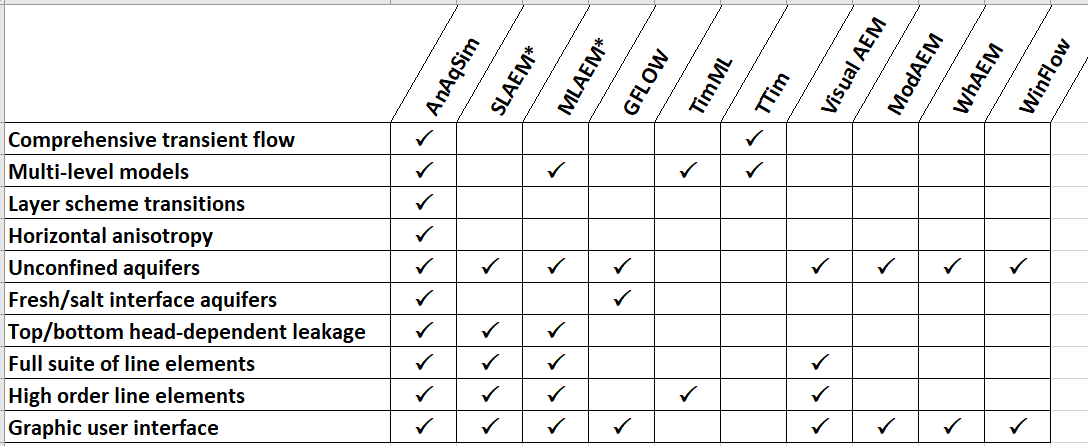
Definitions:
- Comprehensive transient flow: Most things that can be modeled in steady state can also be modeled in transient simulations. Important parameters such as specified heads, discharges, and recharge rates can vary with time during the simulation.
- Multi-level models: Simulation of multiple levels with vertical leakage and resistance between levels, as opposed to single-layer (2D) simulation.
- Layer scheme transitions: Different layering schemes in different regions of the model. For example, a single layer in one area and four layers in the area of interest.
- Horizontal anisotropy: K anisotropy in the plane of the layer, and the angle and ratio can be heterogeneous within a layer.
- Fresh/salt interface aquifers: Aquifers with a sharp fresh-salt interface using the Ghyben-Herzberg equation.
- Top/bottom head-dependent leakage: Recharge or leakage in/out the top or bottom of the model based on head difference from a specified head.
- Full suite of line elements: Line elements for heterogeneity, specified head, specified flux, river, drain, and barrier boundaries.
- High order line elements: Each line segment may have at least 3 degrees of freedom (parameters), the number of which can be adjusted to improve accuracy.
- Graphic user interface: User interface with integrated menus, data entry forms, graphics, etc. Programs without a GUI are run from text commands.